3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
扇形の面積の求め方で側面積を出す → 母線(もとの円の半径)×母線×円周率(π：314)×中心角の大きさ÷360=側面積 ←4 最後に底面積と側面積を足し合わせれば四角錐の表面積が求められます。 扇形の面積を求めるときに困惑する人が多いかもしれません。球の表面積と体積 このテキストでは、球の表面積と体積を求める公式を紹介します。2ページ目には練習問題を入れてあるので、チャレンジしてみてください。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとしたとき、次の式が成
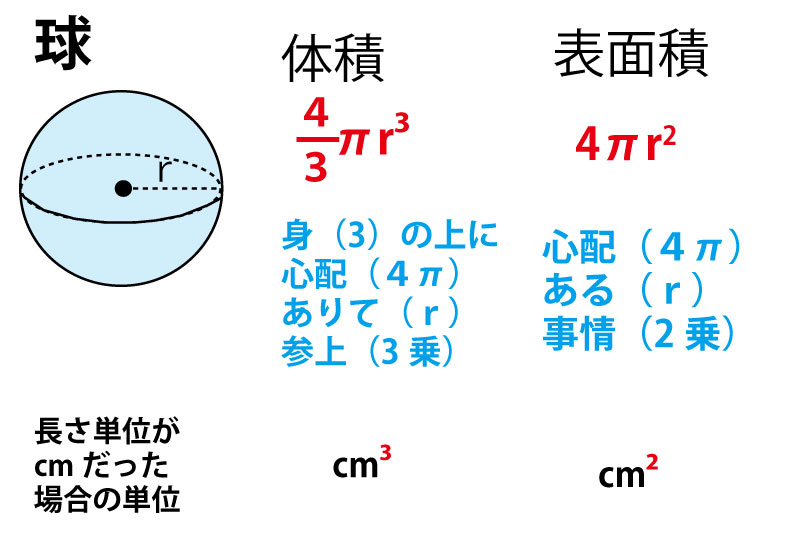
球の体積 表面積 公式 覚え方
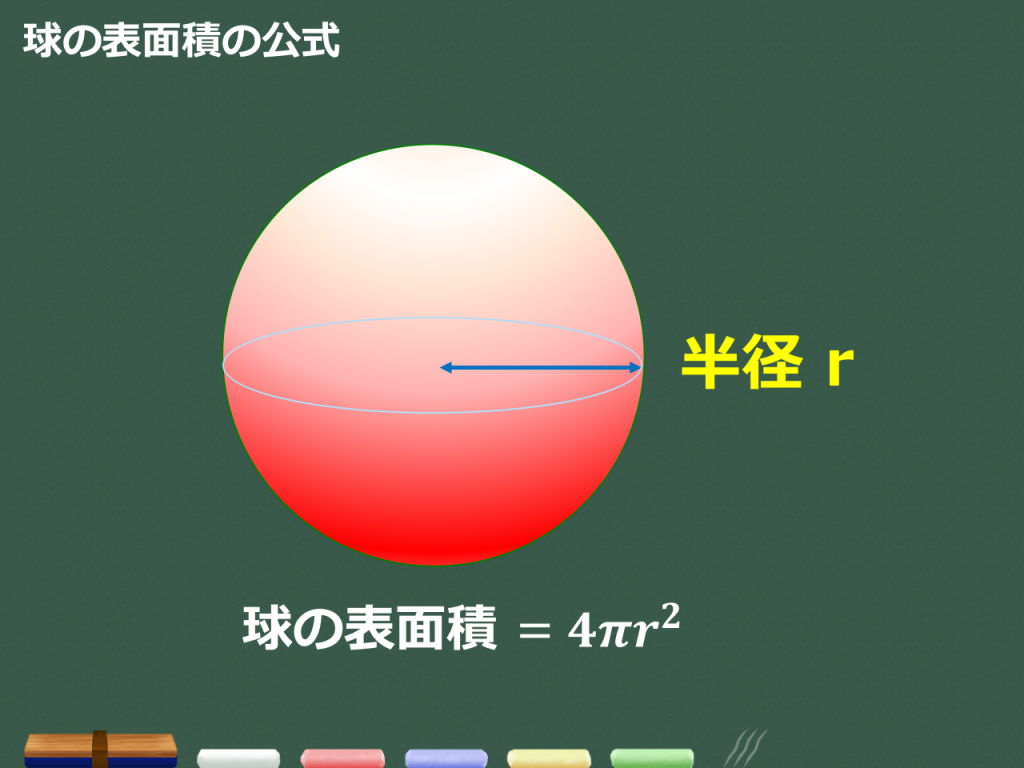
球の体積 表面積 公式 覚え方- 球の表面積の求め方 同様に θ δ θ の点からも円を描き、囲まれた面の面積を求めると、 帯の幅が r δ θ であることを考慮すると、 S = 2 π r cos θ r d θ となる。 ここで d θ → 0 として、限りなく小さくすると、積分で球の表面積を求められる。 式は 球の表面積の求め方公式 半径 r の球の表面積を S とすると、球の表面積 S は次の公式で求められます。 S = 4πr² (例題）半径が4cmの球の表面積を求めましょう。 求める球の表面積を S 、半径を r とすると、 S = 4πr² より S = 4π × 42 ＝ 4π × 16 ＝ 64π
球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館
はがし方① 下図のように切り込みを入れてはがす。 横の長さ＝球の一周分の長さ= 2πr 縦の長さ＝球の半周分の長さ= πr 形を単純にしてだいたいの面積を求める． 面積＝ πr × 2πr × 1 2 = π2r2 ＝ 314πr2 形を切り落として考えているため，実際の面積は 球の表面積は球の体積から求められます。 感覚的な議論になりますが、立体図形を理解する上で重要なポイントが出てきます。 球を「球の中心を頂点とする円錐」の集まりとみなすと、球の体積は球の表面積に半径をかけて3で割った値になります。 なぜ使用目的 創作で、惑星の大きさと居住可能人口を設定するため ご意見・ご感想 漠然と、立方体の辺の長さが2倍になれば大きさが4倍になるのと同じように、球体も直径が2倍になれば表面積も4倍になるかなと思っていたが、実際に計算してみて、間違っていなかったのは少し感動した。
球の体積 表面積 公式 覚え方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも | 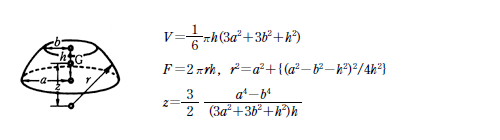 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
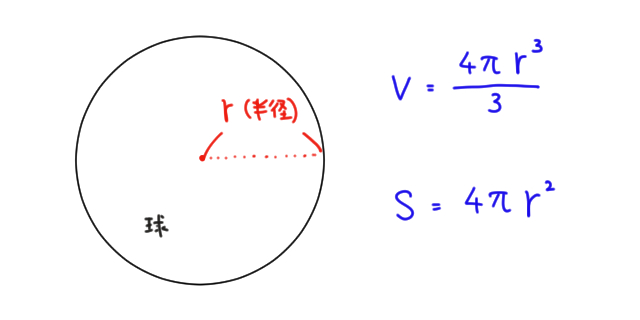 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
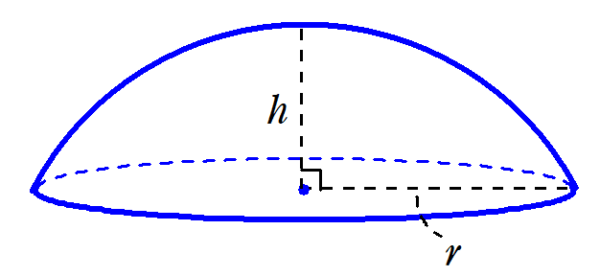 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |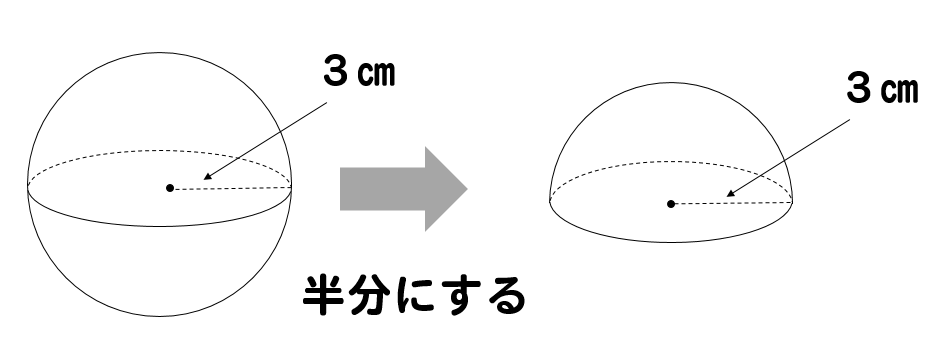
球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも | 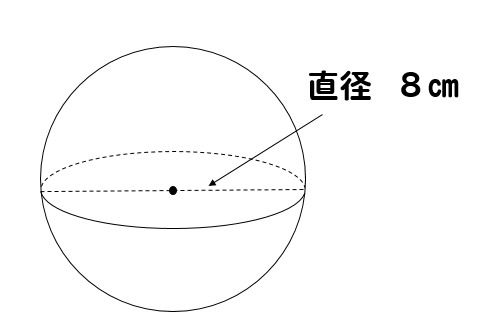 球欠と球冠 Fukusukeの数学めも |
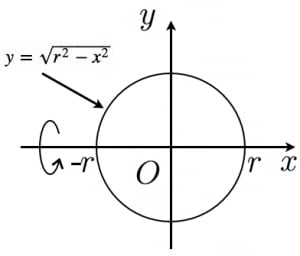 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも | 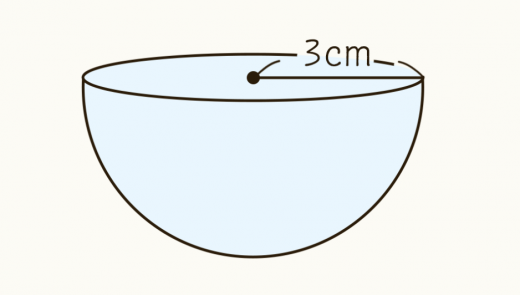 球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも | 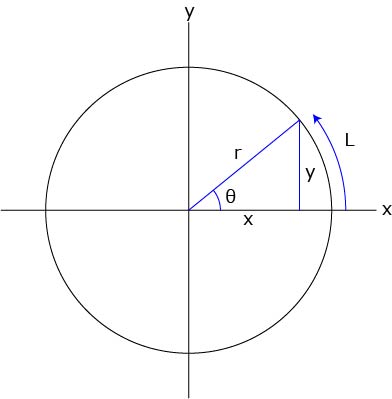 球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも | 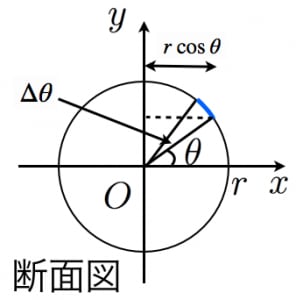 球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも | 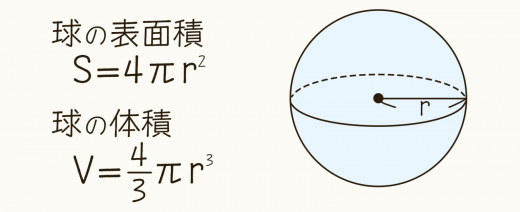 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも | 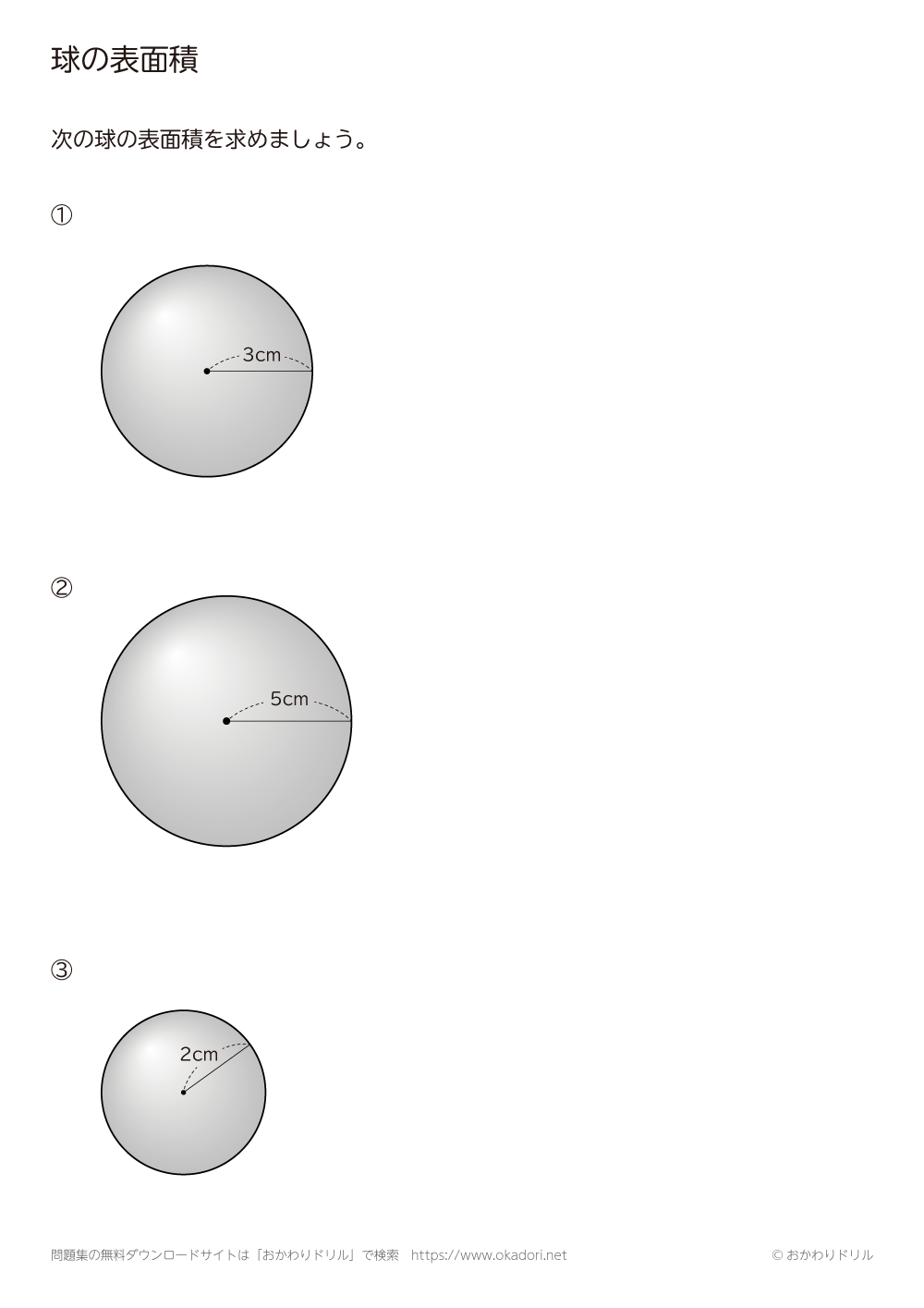 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも | 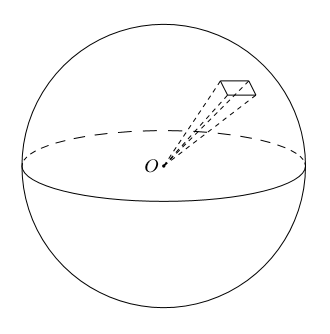 球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも | 球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
「球の体積 表面積 公式 覚え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
 球欠と球冠 Fukusukeの数学めも |  球欠と球冠 Fukusukeの数学めも |
